单调栈
首先可以看下 739.每日温度及496、503下一个更大元素,了解单调栈的妙用。
84. 柱状图中最大的矩形
难度困难
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
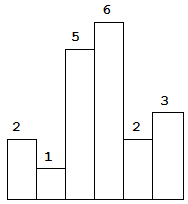
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
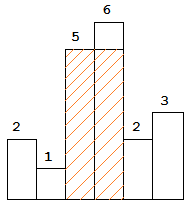
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10函数签名:
func largestRectangleArea(heights []int) int分析
朴素实现
可以枚举所有的宽,对每个宽找到最小对高度求出面积;也可以枚举所有的高(柱子),对每个柱子,向左、向右分别找到不低于当前柱子对柱子,也就确定了宽度,进而可以计算面积。
枚举宽度大体实现:
func largestRectangleArea(heights []int) int {
res := 0
for i := 0; i < len(heights); i++ {
for j := i; j < len(heights); j++ {
width := j-i+1
// 找到闭区间 [i, j] 中对最小高度
height := min(heights[i:j+1])
res = max(res, width*height)
}
}
return res
}枚举高度大体实现:
func largestRectangleArea(heights []int) int {
res := 0
for i, h := range heights {
width := 0
for j := i; j >=0 && heights[j] >= h; j-- {
width++
}
for j := i; j < len(heights); j++ {
width++
}
res = max(res, width*h)
}
return res
}以上两种解法对时间复杂度是 O(n),空间复杂度是 O(1)
借助单调栈优化朴素实现
对于第二个朴素实现,可以借助两个单调递增栈,实现以 O(n) 的代价确定每个位置 i 向左向右扩展低于 heights[i] 的位置;最终将整个时间复杂度降低到 O(n)
func largestRectangleArea(heights []int) int {
res := 0
left, right := calLeft(heights), calRight(heights)
for i, v := range heights {
res = max(res, v*(right[i]-left[i]-1))
}
return res
}
// 计算每个柱子向左延伸,第一个低于当前柱子的柱子位置,可以是 -1
func calLeft(heights []int) []int {
res := make([]int, len(heights))
stack := make([]int, 0, len(heights))
for i, v := range heights {
for len(stack) > 0 && heights[stack[len(stack)-1]] >= v {
stack = stack[:len(stack)-1]
}
if len(stack) == 0 {
res[i] = -1
} else {
res[i] = stack[len(stack)-1]
}
stack = append(stack, i)
}
return res
}
// 计算每个柱子向右延伸,第一个低于当前柱子的位置,可以是 len(heights)
func calRight(heights []int) []int {
res := make([]int, len(heights))
stack := make([]int, 0, len(heights))
for i := len(heights)-1; i >= 0; i-- {
for len(stack) > 0 && heights[stack[len(stack)-1]] >= heights[i] {
stack = stack[:len(stack)-1]
}
if len(stack) == 0 {
res[i] = len(heights)
} else {
res[i] = stack[len(stack)-1]
}
stack = append(stack, i)
}
return res
}85. 最大矩形
难度困难
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。示例 2:
输入:matrix = []
输出:0示例 3:
输入:matrix = [["0"]]
输出:0示例 4:
输入:matrix = [["1"]]
输出:1示例 5:
输入:matrix = [["0","0"]]
输出:0提示:
rows == matrix.lengthcols == matrix[0].length0 <= row, cols <= 200matrix[i][j]为'0'或'1'
分析
可以枚举所有的矩形,查看是否所有格子都是 1。可以枚举所有的左上角和对应的右下角来确定一个矩形。整个时间复杂度是 O(n^2 * m^2), 其中 n, m 分别是矩阵行数及列数。
实际上这个问题可以划归为上一个问题,以题目中示例一为例:

列方向连续的格子 1 形成了一个个柱子,只需要逐行向下,每次更新 heights,再使用上一题的解法更新结果即可。这样整个时间复杂度降低到了 O(n*m)
var left, right, height, stack []int
var res int
func maximalRectangle(matrix [][]byte) int {
if len(matrix) == 0 || len(matrix[0]) == 0 {
return 0
}
reset(len(matrix[0]))
for _, row := range matrix {
calHeight(row)
calLeft()
calRight()
calRes()
}
return res
}
func reset(n int) {
left = make([]int, n)
right = make([]int, n)
height = make([]int, n)
stack = make([]int, n)
res = 0
}
func calHeight(row []byte) {
for i, v := range row {
if v == '1' {
height[i]++
} else {
height[i] = 0
}
}
}
func calLeft() {
stack = stack[:0]
for i, v := range height {
for len(stack) > 0 && height[stack[len(stack)-1]] >= v {
stack = stack[:len(stack)-1]
}
if len(stack) == 0 {
left[i] = -1
} else {
left[i] = stack[len(stack)-1]
}
stack = append(stack, i)
}
}
func calRight() {
stack = stack[:0]
for i := len(height)-1; i >= 0; i-- {
v := height[i]
for len(stack) > 0 && height[stack[len(stack)-1]] >= v {
stack = stack[:len(stack)-1]
}
if len(stack) == 0 {
right[i] = len(height)
} else {
right[i] = stack[len(stack)-1]
}
stack = append(stack, i)
}
}
func calRes() {
for i, v := range height {
tmp := v *(right[i]-left[i]-1)
if tmp > res {
res = tmp
}
}
}