遍历二维矩阵
对于二维矩阵,可以按照有趣的顺序遍历, 如下所示的“方形水波”、螺旋、对角线等几种遍历方法。
1030. 距离顺序排列矩阵单元格
难度简单
给出 R 行 C 列的矩阵,其中的单元格的整数坐标为 (r, c),满足 0 <= r < R 且 0 <= c < C。
另外,我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。
返回矩阵中的所有单元格的坐标,并按到 (r0, c0) 的距离从最小到最大的顺序排,其中,两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)
示例 1:
输入:R = 1, C = 2, r0 = 0, c0 = 0
输出:[[0,0],[0,1]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1]示例 2:
输入:R = 2, C = 2, r0 = 0, c0 = 1
输出:[[0,1],[0,0],[1,1],[1,0]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。示例 3:
输入:R = 2, C = 3, r0 = 1, c0 = 2
输出:[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2,2,3]
其他满足题目要求的答案也会被视为正确,例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。提示:
1 <= R <= 1001 <= C <= 1000 <= r0 < R0 <= c0 < C
函数签名:
func allCellsDistOrder(R int, C int, r0 int, c0 int) [][]int分析
最直观也是最高效的解法,可以称作“方形水波遍历”。
func allCellsDistOrder(R int, C int, r0 int, c0 int) [][]int {
result := make([][]int, R*C)
result[0] = []int{r0, c0}
step := 1
r, c := r0, c0
for step < R*C {
r-- // 从上一次遍历后的方形水波上顶点再上一步到达这次需要遍历的方形水波上顶点
for r < r0 { // 上顶点 -> 右顶点
if r >= 0 && c <= C-1 {
result[step] = []int{r, c}
step++
}
r++
c++
}
for c > c0 { // 右顶点 -> 下顶点
if r <= R-1 && c <= C-1 {
result[step] = []int{r, c}
step++
}
r++
c--
}
for r > r0 { // 下顶点 -> 左顶点
if r <= R-1 && c >= 0 {
result[step] = []int{r, c}
step++
}
r--
c--
}
for c < c0 { // 左顶点 -> 上顶点 // 这里的判断是c<c0, 保证了不会将上顶点重复放入结果
if r >= 0 && c >= 0 {
result[step] = []int{r, c}
step++
}
r--
c++
}
}
return result
}54. 螺旋矩阵
难度中等
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]示例 2:

输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
分析
维护边界
// 直觉遍历,时空复杂度都是O(m*n)
func spiralOrder(matrix [][]int) []int {
if len(matrix) == 0 || len(matrix[0]) == 0 {
return nil
}
const right, down, left, up = 0, 1, 2, 3
m, n := len(matrix), len(matrix[0])
rMin, rMax, cMin, cMax := 0, m-1, 0, n-1 // 上下左右边界
r, c, direct := 0, 0, right
res := make([]int, m*n)
for i := range res {
res[i] = matrix[r][c]
switch direct {
case right:
if c < cMax {
c++
} else {
direct, rMin, r = down, rMin+1, r+1
}
case down:
if r < rMax {
r++
} else {
direct, cMax, c = left, cMax-1, c-1
}
case left:
if c > cMin {
c--
} else {
direct, rMax, r = up, rMax-1, r-1
}
case up:
if r > rMin {
r--
} else {
direct, cMin, c = right, cMin+1, c+1
}
}
}
return res
}维护层
if len(matrix) == 0 || len(matrix[0]) == 0 {
return nil
}
m, n := len(matrix), len(matrix[0])
levels := (min(m, n) + 1) / 2 //层数
res := make([]int, 0, m*n)
// 从外层向内层层层遍历
for i := 0; i < levels; i++ {
for c := i; c < n-i; c++ { // 向右
res = append(res, matrix[i][c])
}
for r := i + 1; r < m-i; r++ { // 向下
res = append(res, matrix[r][n-1-i])
}
for c := n - 1 - (i + 1); m-1-i != i && c >= i; c-- { // 向左;可能这一层只有一行,注意判断m-1-i 与 i是否相等
res = append(res, matrix[m-1-i][c])
}
for j := m - 1 - (i + 1); n-1-i != i && j >= i+1; j-- { // 向上;可能这一层只有一列,注意判断n-1-i 与 i是否相等
res = append(res, matrix[j][i])
}
}
return res
}498. 对角线遍历
难度中等
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
解释:说明:
- 给定矩阵中的元素总数不会超过 100000 。
分析
二维矩阵对角线上的坐标有规律:
每条主对角线上的横纵坐标之和为定值,副对角线上的横纵坐标之差为定值。
比如这个问题里的主对角线。
1。每一趟对角线中元素的坐标(r,c), r+c 的值是递增的,且正好是遍历的趟数——r代表行,c代表列。
第0趟:r+c == 0
第1趟:r+c == 1
第2趟:r+c == 2
第3趟:r+c == 3
第4趟:r+c == 4
。。。
且趟数上限是m+n-2(即m-1 + n-1)
2。每一趟,要么横坐标递增,纵坐标递减;要么横坐标递减,纵坐标递增。
第0趟:r,c都是从0到0
第1趟:r从0到1,c从1到0
第2趟:r从2到0,c从0到2
第3趟:r从1到2,c从2到1
第4趟:r和c都是从2到2
即偶数趟从左下到右上,r递减,c递增;奇数趟从右上到左下r递增,c递减func findDiagonalOrder(matrix [][]int) []int {
if len(matrix) == 0 || len(matrix[0]) == 0 {
return nil
}
m, n := len(matrix), len(matrix[0])
res := make([]int, m*n)
i := 0
for time := 0; time <= m+n-2; time++ {
if time%2 == 0 { // 偶数趟,r递减
r := min(time, m-1)
c := time - r
for r >= 0 && c < n {
res[i] = matrix[r][c]
i++
r--
c++
}
} else { // 奇数趟, c递减
c := min(time, n-1)
r := time - c
for c >= 0 && r < m {
res[i] = matrix[r][c]
i++
c--
r++
}
}
}
return res
}1329. 将矩阵按对角线排序
难度中等
给你一个 m * n 的整数矩阵 mat ,请你将同一条对角线上的元素(从左上到右下)按升序排序后,返回排好序的矩阵。
示例 1:
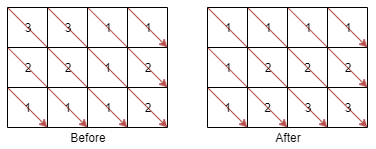
输入:mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出:[[1,1,1,1],[1,2,2,2],[1,2,3,3]]提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1001 <= mat[i][j] <= 100
分析
二维矩阵副对角线上的坐标有一个特点,对于每一条对角线,横坐标与纵坐标差为定值。
可以用横坐标与纵坐标差来标识每条对角线。显然其是从 m-1 到 1-n 的连续序列。
借助哈希表
func diagonalSort(mat [][]int) [][]int {
m, n := len(mat), len(mat[0])
diagonals := make(map[int][]int, m+n-1)
for r, row := range mat {
for c, val := range row {
diagonals[r-c] = append(diagonals[r-c], val)
}
}
for k := range diagonals {
sort.Ints(diagonals[k])
}
res := make([][]int, m)
for r := range res {
res[r] = make([]int, n)
for c := range res[r] {
res[r][c] = diagonals[r-c][0]
diagonals[r-c] = diagonals[r-c][1:]
}
}
return res
}不用哈希表
func diagonalSort(mat [][]int) [][]int {
m, n := len(mat), len(mat[0])
res := make([][]int, m)
for i := range res {
res[i] = make([]int, n)
}
for i := m - 1; i >= 1-n; i-- {
r := max(i, 0)
c := r - i
size := min(m-r, n-c)
tmp := make([]int, size)
// add elements into tmp from top-left to bottom-right
for k := range tmp {
tmp[k] = mat[r][c]
r++
c++
}
// add sorted elements into res from top-left to bottom-right
sort.Ints(tmp)
r = max(i, 0)
c = r - i
for k := range tmp {
res[r][c] = tmp[k]
r++
c++
}
}
return res
}[59] 螺旋矩阵 II
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3
输出:
[
[ 1, 2, 3 ],
[ 8, 9, 4 ],
[ 7, 6, 5 ]
]分析
与上个问题非常类似,不妨借用上个问题的第二个解法:
func generateMatrix(n int) [][]int {
if n <= 0 {
return nil
}
res := make([][]int, n)
for i := range res {
res[i] = make([]int, n)
}
levels := (n + 1) / 2
num := 1
for i := 0; i < levels; i++ {
for c := i; c < n-i; c++ {
res[i][c] = num
num++
}
for r := i + 1; r < n-i; r++ {
res[r][n-1-i] = num
num++
}
for c := n - 2 - i; i != n-1-i && c >= i; c-- {
res[n-1-i][c] = num
num++
}
for r := n - 2 - i; i != n-1-i && r > i; r-- {
res[r][i] = num
num++
}
}
return res
}[885] 螺旋矩阵 III
在 R 行 C 列的矩阵上,我们从 (r0, c0) 面朝东面开始
这里,网格的西北角位于第一行第一列,网格的东南角位于最后一行最后一列。
现在,我们以顺时针按螺旋状行走,访问此网格中的每个位置。
每当我们移动到网格的边界之外时,我们会继续在网格之外行走(但稍后可能会返回到网格边界)。
最终,我们到过网格的所有 R * C 个空间。
按照访问顺序返回表示网格位置的坐标列表。
示例 1:
输入:R = 1, C = 4, r0 = 0, c0 = 0
输出:[[0,0],[0,1],[0,2],[0,3]]
示例 2:
输入:R = 5, C = 6, r0 = 1, c0 = 4
输出:[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
提示:
1 <= R <= 100
1 <= C <= 100
0 <= r0 < R
0 <= c0 < C分析
模拟即可。借助用一个变量来记录每次向同一个方向走的步长。
var row, column int
func spiralMatrixIII(R int, C int, r int, c int) [][]int {
steps := 0
row, column = R, C
res := make([][]int, 0, R*C)
res = append(res, []int{r, c})
for len(res) < cap(res) {
originR, originC := r, c
// right
steps++
for k := 0; c < C && k < steps && len(res) < cap(res); k++ {
c++
res = checkToAppend(res, r, c)
}
c = originC + steps
// down
for k := 0; r < R && k < steps && len(res) < cap(res); k++ {
r++
res = checkToAppend(res, r, c)
}
r = originR + steps
// left
steps++
for k := 0; c >= 0 && k < steps && len(res) < cap(res); k++ {
c--
res = checkToAppend(res, r, c)
}
c = originC - 1
// up
for k := 0; r >= 0 && k < steps && len(res) < cap(res); k++ {
r--
res = checkToAppend(res, r, c)
}
r = originR - 1
}
return res
}
func checkToAppend(res [][]int, r, c int) [][]int {
if isValid(r, c) {
res = append(res, []int{r, c})
}
return res
}
func isValid(r, c int) bool {
return r >= 0 && r < row && c >= 0 && c < column
}重复代码较多,可优化:
var row, column int
var dirs = [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
func spiralMatrixIII(R int, C int, r int, c int) [][]int {
// right, down, left, up
steps := 0
row, column = R, C
res := make([][]int, 0, R*C)
res = append(res, []int{r, c})
for len(res) < cap(res) {
for i, d := range dirs {
if i == 0 || i == 2 {
steps++
}
for k := 0; k < steps; k++ {
r, c = r+d[0], c+d[1]
res = checkToAppend(res, r, c)
}
}
}
return res
}
func checkToAppend(res [][]int, r, c int) [][]int {
if isValid(r, c) {
res = append(res, []int{r, c})
}
return res
}
func isValid(r, c int) bool {
return r >= 0 && r < row && c >= 0 && c < column
}注意这次代码简单了,但是循环有一些没有及时 break 的地方。