2013. 检测正方形
2013. 检测正方形
| Category | Difficulty | Likes | Dislikes |
|---|---|---|---|
| algorithms | Medium (56.57%) | 119 | - |
给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法:
- 添加 一个在数据流中的新点到某个数据结构中。可以添加 重复 的点,并会视作不同的点进行处理。
- 给你一个查询点,请你从数据结构中选出三个点,使这三个点和查询点一同构成一个 面积为正 的 轴对齐正方形 ,统计 满足该要求的方案数目。
轴对齐正方形 是一个正方形,除四条边长度相同外,还满足每条边都与 x-轴 或 y-轴 平行或垂直。
实现 DetectSquares 类:
DetectSquares()使用空数据结构初始化对象void add(int[] point)向数据结构添加一个新的点point = [x, y]int count(int[] point)统计按上述方式与点point = [x, y]共同构造 轴对齐正方形 的方案数。
示例:
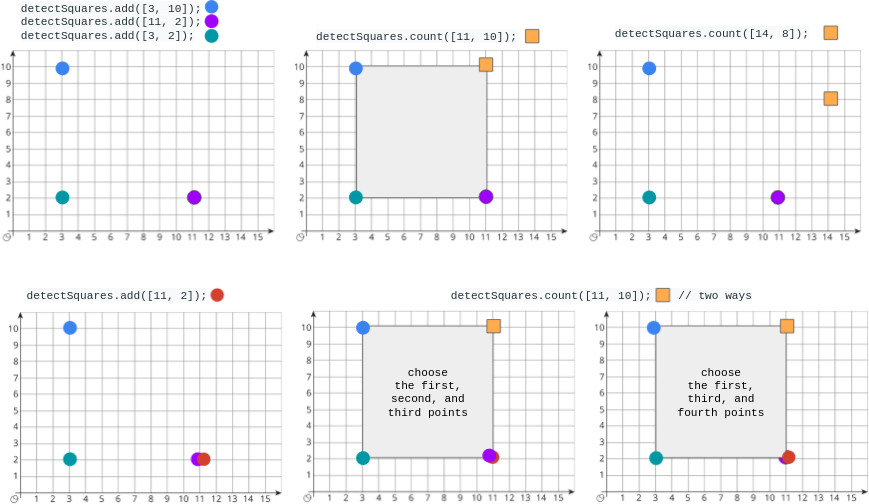
输入:
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
输出:
[null, null, null, null, 1, 0, null, 2]
解释:
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择:
// - 第一个,第二个,和第三个点
detectSquares.count([14, 8]); // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]); // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择:
// - 第一个,第二个,和第三个点
// - 第一个,第三个,和第四个点提示:
point.length == 20 <= x, y <= 1000- 调用
add和count的 总次数 最多为5000
分析
哈希表
可以横坐标为键存储所有的点,注意重复的点,需要记录点点个数。
type Counter map[int]int
type DetectSquares map[int]Counter
func Constructor() DetectSquares {
return DetectSquares{}
}
// 时间复杂度 O(1)
func (ds DetectSquares) Add(point []int) {
x, y := point[0], point[1]
if ds[x] == nil {
ds[x] = Counter{}
}
ds[x][y]++
}
// 最坏情况时间复杂度 O(n),即遍历所有点
func (ds DetectSquares) Count(point []int) int {
res := 0
px, py := point[0], point[1]
for y, cnt := range ds[px] {
dis := py - y
if dis == 0 {
continue
}
res += ds[px-dis][y] * ds[px-dis][py] * cnt
res += ds[px+dis][y] * ds[px+dis][py] * cnt
}
return res
}