1514. 概率最大的路径
1514. 概率最大的路径 (Medium)
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5,就会被视作正确答案。
示例 1:
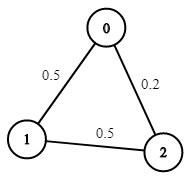
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25示例 2:
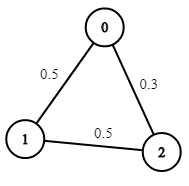
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出:0.30000示例 3:
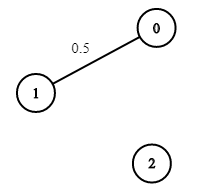
输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出:0.00000
解释:节点 0 和 节点 2 之间不存在路径提示:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- 每两个节点之间最多有一条边
分析
先想到记忆化搜索的解法,不过这个思路是是错误的。
func maxProbability(n int, edges [][]int, succProb []float64, start int, end int) float64 {
type Node struct {
to int
prob float64
}
graph := make([][]Node, n)
for i, e := range edges {
u, v, p := e[0], e[1], succProb[i]
graph[u] = append(graph[u], Node{to: v, prob: p})
graph[v] = append(graph[v], Node{to: u, prob: p})
}
memo := make([]float64, n)
for i := range memo {
memo[i] = -1
}
vis := make([]bool, n)
var dfs func(node int) float64
dfs = func(node int) float64 {
if node == end {
return 1
}
if memo[node] > -1 {
return memo[node]
}
vis[node] = true
res := 0.0
for _, next := range graph[node] {
if vis[next.to] {
continue
}
res = math.Max(res, dfs(next.to)*next.prob)
}
vis[node] = false
memo[node] = res
return res
}
return dfs(start)
}这是因为 vis 干扰了后续计算。
比如:
0
/ \
1 - 2
\ /
3起点为 0, 终点为 3
在计算过程中,0->2->1->3 这个路径会被漏掉
正解是 Dijkstra 算法,即基于堆的 BFS 贪心解法。
func maxProbability(n int, edges [][]int, succProb []float64, start int, end int) float64 {
graph := make([][]State, n)
for i, e := range edges {
u, v, p := e[0], e[1], succProb[i]
graph[u] = append(graph[u], State{node: v, prob: p})
graph[v] = append(graph[v], State{node: u, prob: p})
}
memo := make([]float64, n)
h := &Heap{}
h.push(State{node: start, prob: 1.0})
for h.Len() > 0 {
cur := h.pop()
if cur.node == end {
return cur.prob
}
for _, next := range graph[cur.node] {
if memo[next.node] >= next.prob*cur.prob {
continue
}
memo[next.node] = next.prob * cur.prob
h.push(State{node: next.node, prob: next.prob * cur.prob})
}
}
return 0
}
type State struct {
node int
prob float64
}
type Heap struct {
s []State
}
func (h *Heap) Len() int { return len(h.s) }
func (h *Heap) Less(i, j int) bool { return h.s[i].prob > h.s[j].prob }
func (h *Heap) Swap(i, j int) { h.s[i], h.s[j] = h.s[j], h.s[i] }
func (h *Heap) Push(x any) { h.s = append(h.s, x.(State)) }
func (h *Heap) Pop() any {
n := len(h.s)
x := h.s[n-1]
h.s = h.s[:n-1]
return x
}
func (h *Heap) push(s State) { heap.Push(h, s) }
func (h *Heap) pop() State { return heap.Pop(h).(State) }