1937. 扣分后的最大得分

题解

1937. 扣分后的最大得分

难度中等

给你一个 m x n 的整数矩阵 points （下标从 0 开始）。一开始你的得分为 0 ，你想最大化从矩阵中得到的分数。

你的得分方式为：每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分增加 points[r][c] 。

然而，相邻行之间被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为 (r, c1) 和 (r + 1, c2) 的格子，你的总得分减少 abs(c1 - c2) 。

请你返回你能得到的最大得分。

abs(x) 定义为：

如果 x >= 0 ，那么值为 x 。
如果 x < 0 ，那么值为 -x 。

示例 1：

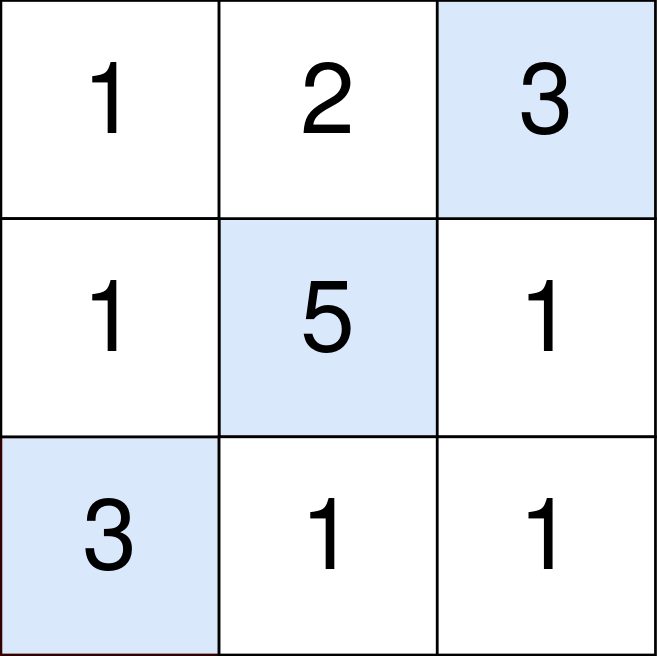
输入： points = [[1,2,3],[1,5,1],[3,1,1]] 输出： 9 解释： 蓝色格子是最优方案选中的格子，坐标分别为 (0, 2)，(1, 1) 和 (2, 0) 。你的总得分增加 3 + 5 + 3 = 11 。但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。你的最终得分为 11 - 2 = 9 。

示例 2：

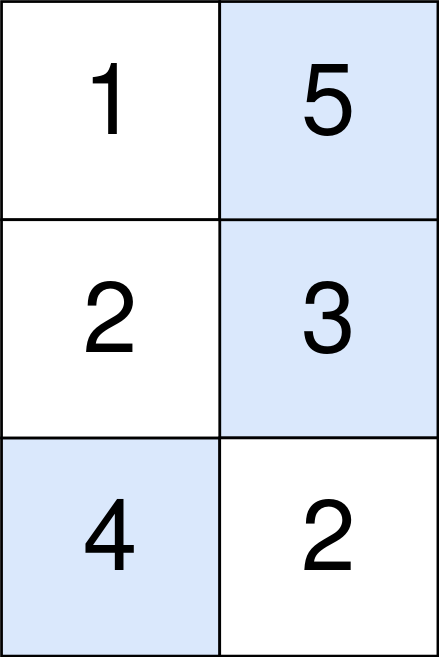
输入： points = [[1,5],[2,3],[4,2]] 输出： 11 解释： 蓝色格子是最优方案选中的格子，坐标分别为 (0, 1)，(1, 1) 和 (2, 0) 。你的总得分增加 5 + 3 + 4 = 12 。但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。你的最终得分为 12 - 1 = 11 。

提示：

m == points.length
n == points[r].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
0 <= points[r][c] <= 10^5

函数签名：

func maxPoints(points [][]int) int64

分析

动态规划

不难想到动态规划解法：

func maxPoints(points [][]int) int64 {
    m, n := len(points), len(points[0])
    dp := make([]int64, n)
    pre := make([]int64, n)
    for i, v := range points[0] {
        dp[i] = int64(v)
    }
    for r := 1; r < m; r++ {
        pre, dp = dp, pre
        for c := 0; c < n; c++ {
            var tmp int64 = 0
            for c1 := 0; c1 < n; c1++ {
                tmp = max(tmp, pre[c1]-abs(int64(c-c1)))
            }
            dp[c] = tmp+int64(points[r][c])
        }
    }
    var res int64 = 0
    for _, v := range dp {
        res = max(res, v)
    }
    return res
}

func max(a, b int64) int64 {
    if a > b {
        return a
    }
    return b
}

func abs(x int64) int64 {
    if x < 0 {
        return -x
    }
    return x
}

时间复杂度是：$O(mn^2)$，有点高。能不能优化呢？

我们的转移方程是：

$dp[c] = max(pre[c’]- |c-c’|) + points[r][c]$

可以去掉绝对值符号，转化为：

$c \geq c’$ 时，$dp[c] = max(pre[c’] + c’ - c) + points[r][c]$, 即 $dp[c] = max(pre[c’] + c’) + points[r][c]- c$ ;

$c < c’$ 时，$dp[c] = max(pre[c’] - c’ + c) + points[r][c]$, 即 $dp[c] = max(pre[c’] - c’) + points[r][c] + c$ .

这意味着对于第 $c$ 列，需要在左侧找到最大的 $pre[c’]+c’$，在右侧找到最大的 $pre[c’] - c’$ . 即需要维护前后缀最大值。

func maxPoints(points [][]int) int64 {
    m, n := len(points), len(points[0])
    dp := make([]int64, n)
    pre := make([]int64, n)
    for i, v := range points[0] {
        dp[i] = int64(v)
    }
    for r := 1; r < m; r++ {
        pre, dp = dp, pre
        var preMax int64 = math.MinInt64
        for c := 0; c < n; c++ {
            preMax = max(preMax, pre[c]+int64(c))
            dp[c] = max(dp[c], preMax+int64(points[r][c]-c))
        }
        var sufMax int64 = math.MinInt64
        for c := n-1; c >= 0; c-- {
            sufMax = max(sufMax, pre[c]-int64(c))
            dp[c] = max(dp[c], sufMax+int64(points[r][c]+c))
        }
    }
    var res int64
    for _, v := range dp {
        res = max(res, v)
    }
    return res
}

func max(a, b int64) int64 {
    if a > b {
        return a
    }
    return b
}

func abs(x int64) int64 {
    if x < 0 {
        return -x
    }
    return x
}

时间复杂度是：$O(mn)$，空间复杂度：$O(n)$ 。

剑指 Offer 60. n个骰子的点数 LCOF 1962. 移除石子使总数最小