756. 金字塔转换矩阵

题解

756. 金字塔转换矩阵

中等， 55%

你正在把积木堆成金字塔。每个块都有一个颜色，用一个字母表示。每一行的块比它下面的行 少一个块 ，并且居中。

为了使金字塔美观，只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的，其中模式的前两个字符分别表示左右底部块，第三个字符表示顶部块。

例如，"ABC" 表示一个三角形图案，其中一个 “C” 块堆叠在一个 'A' 块(左)和一个 'B' 块(右)之上。请注意，这与 "BAC" 不同，"B" 在左下角，"A" 在右下角。

你从底部的一排积木 bottom 开始，作为一个单一的字符串，你必须使用作为金字塔的底部。

在给定 bottom 和 allowed 的情况下，如果你能一直构建到金字塔顶部，使金字塔中的 每个三角形图案 都是允许的，则返回 true ，否则返回 false 。

示例 1：

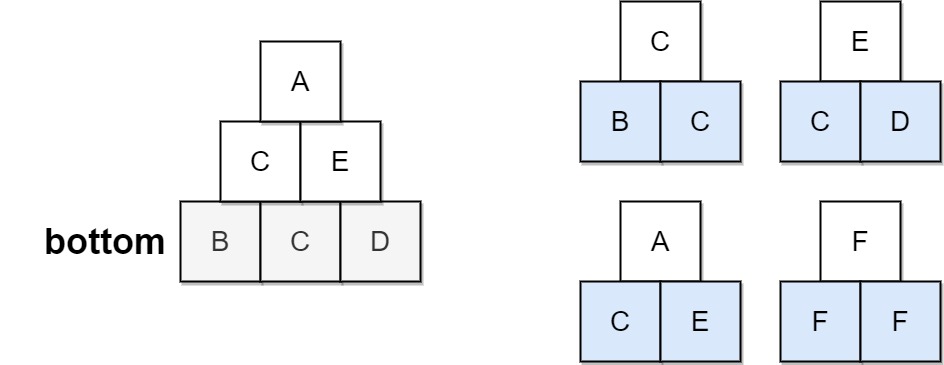
输入：bottom = "BCD", allowed = ["BCG", "CDE", "GEA", "FFF"]
输出：true
解释：允许的三角形模式显示在右边。
从最底层(第3层)开始，我们可以在第2层构建“CE”，然后在第1层构建“E”。
金字塔中有三种三角形图案，分别是“BCC”、“CDE”和“CEA”。都是允许的。

示例 2：

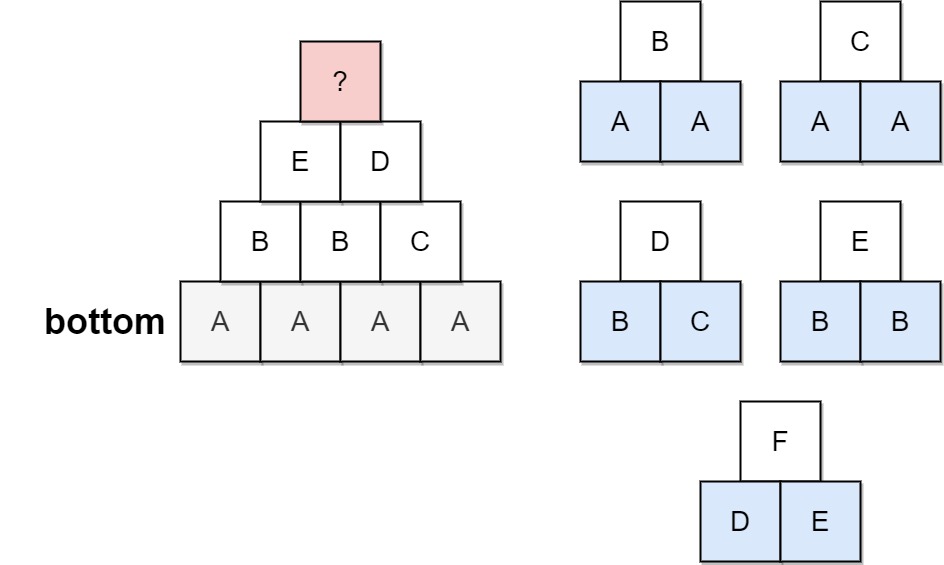
输入：bottom = "AABA", allowed = ["AAA", "AAB", "ABA", "ABB", "BAC"]
输出：false
解释：允许的三角形模式显示在右边。
从最底层(游戏邦注:即第4个关卡)开始，创造第3个关卡有多种方法，但如果尝试所有可能性，你便会在创造第1个关卡前陷入困境。

提示：

2 <= bottom.length <= 6
0 <= allowed.length <= 216
allowed[i].length == 3
所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F', 'G'}。
allowed 中所有值都是 唯一的

函数签名：

func pyramidTransition(bottom string, allowed []string) bool

分析

常规DFS

用 dfs 模拟构建金字塔即可。为了方便编码，可以定义函数 dfs(cur, next string) bool 表示对于当前行 cur，是否能构建出一个金字塔，next 用来辅助。

为了方便操作字符，参数类型 string 可以改成 []byte

对于两个字母，上层能放哪些字母？信息包含在 allowed 数组里，可以预处理成一个 map，来迅速获知。

func pyramidTransition(bottom string, allowed []string) bool {
    nexts := map[string][]byte{}
    for _, v := range allowed {
        nexts[v[:2]] = append(nexts[v[:2]], v[2])
    }

    var dfs func(cur, next []byte) bool
    dfs = func(cur, next []byte) bool {
        if len(cur) == 1 {
            return true
        }
        if len(cur) == len(next)+1 {
            return dfs(next, nil)
        }
        i := len(next)
        s := string(cur[i : i+2])
        for _, c := range nexts[s] {
            if dfs(cur, append(next, c)) {
                return true
            }
        }
        return false
    }

    return dfs([]byte(bottom), nil)
}

时间复杂度不太好分析。Leetcode 实测结果 600 ms，在超时的边缘。

优化的DFS

常规 DFS 里的 next 耗费的空间很多，且隐含着回溯逻辑。实际上，在这个问题里，无须回溯。

首先去掉 next，仅保留 cur，一直复用 cur来优化空间复杂度，另用一个整形变量 i 代表 next的长度。

func pyramidTransition(bottom string, allowed []string) bool {
    nexts := map[string][]byte{}
    for _, v := range allowed {
        nexts[v[:2]] = append(nexts[v[:2]], v[2])
    }

    var dfs func(cur []byte, i int) bool
    dfs = func(cur []byte, i int) bool {
        if len(cur) == 1 {
            return true
        }
        if len(cur) == i+1 {
            return dfs(cur[:len(cur)-1], 0)
        }
        s := string(cur[i : i+2])
        for _, c := range nexts[s] {
            cur[i] = c // no need to backtrack
            if dfs(cur, i+1) {
                return true
            }
        }
        return false
    }

    return dfs([]byte(bottom), 0)
}

时间复杂度：$O(n^2*m)$， $n$ 指 bottom的长度，$m$ 指 allowed 的长度。Leetcode 实测结果 0 ms。

小结

优化的关键在于发现构建过程无须回溯。

扩展

题目里有一个约束：

所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F', 'G'}

可以用一个字节来表示某个字符串，进而减少nexts 的大小；但会增加编码复杂度。

576. 出界的路径数通配符/模式匹配