576. 出界的路径数
576. 出界的路径数
难度中等
给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内(可以穿过网格边界到达网格之外)。你 最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ,找出并返回可以将球移出边界的路径数量。因为答案可能非常大,返回对 $10^9+7$ 取余 后的结果。
示例 1:
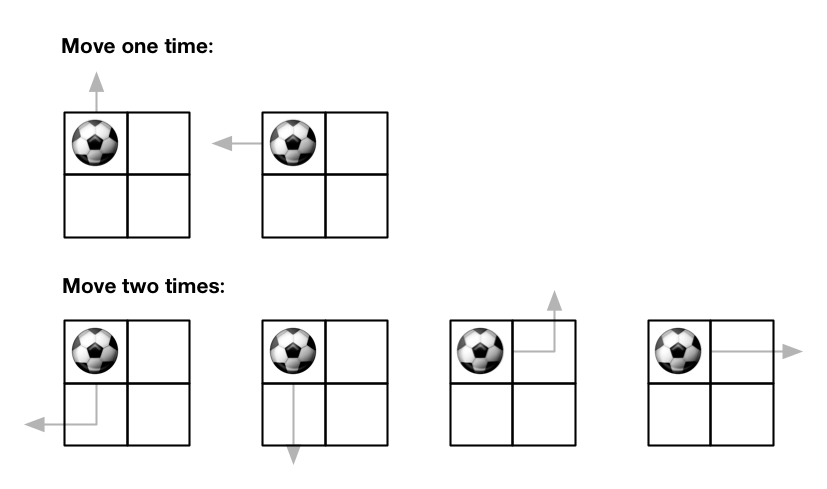
输入: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 输出: 6
示例 2:
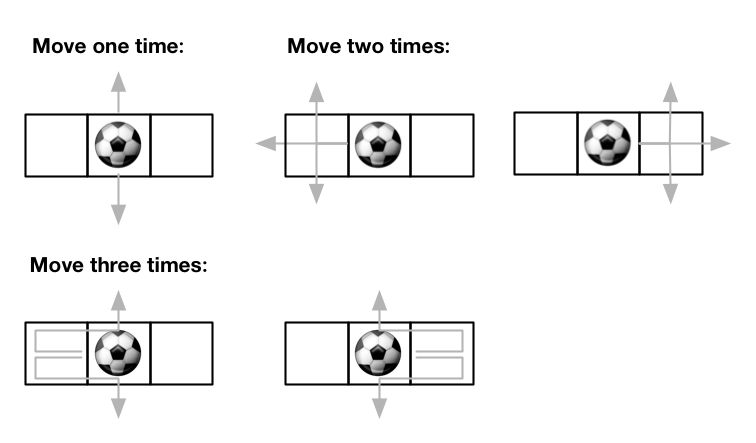
输入: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 输出: 12
提示:
1 <= m, n <= 500 <= maxMove <= 500 <= startRow < m0 <= startColumn < n
分析
DFS 暴力解
func findPaths(m int, n int, maxMove int, startRow int, startColumn int) int {
const mod = 1e9+7
dirs := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
// dfs 返回在(r, c) 位置,还有 left 步可以走时能够走到界外的可能路径数
var dfs func(r, c, left int) int
dfs = func(r, c, left int) int {
if r == -1 || r == m || c == -1 || c == n {
return 1
}
if left == 0 {
return 0
}
res := 0
for _, d := range dirs {
res = (res+dfs(r+d[0], c+d[1], left-1)) % mod
}
return ans
}
return dfs(startRow, startColumn, maxMove)
}暴力 DFS 会超时,对于同样的 (r, c, left),存在重复计算。
DFS + 备忘录 (记忆化搜索)
可以为暴力 DFS 加上备忘录,避免重复计算
func findPaths(m int, n int, maxMove int, startRow int, startColumn int) int {
const mod = 1e9+7
memo := make([][][]int, m)
for i := range memo {
memo[i] = make([][]int, n)
for j := range memo[i] {
memo[i][j] = make([]int, maxMove+1)
for k := range memo[i][j] {
memo[i][j][k] = -1
}
}
}
dirs := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
var dfs func(r, c, left int) int
dfs = func(r, c, left int) int {
if r == -1 || r == m || c == -1 || c == n {
return 1
}
if left == 0 {
return 0
}
if memo[r][c][left] != -1 {
return memo[r][c][left]
}
res := 0
for _, d := range dirs {
res = (res+dfs(r+d[0], c+d[1], left-1)) % mod
}
memo[r][c][left] = res
return memo[r][c][left]
}
return dfs(startRow, startColumn, maxMove)
}时间、空间复杂的都是 $o(m \times n \times maxMove)$