1601. 最多可达成的换楼请求数目
1601. 最多可达成的换楼请求数目
难度困难
我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。
给你一个数组 requests ,其中 requests[i] = [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。
一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ,一个员工要离开楼 1 ,一个员工要离开楼 2 ,如果该请求列表可行,应该要有两个员工搬入楼 0 ,一个员工搬入楼 1 ,一个员工搬入楼 2 。
请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。
示例 1:
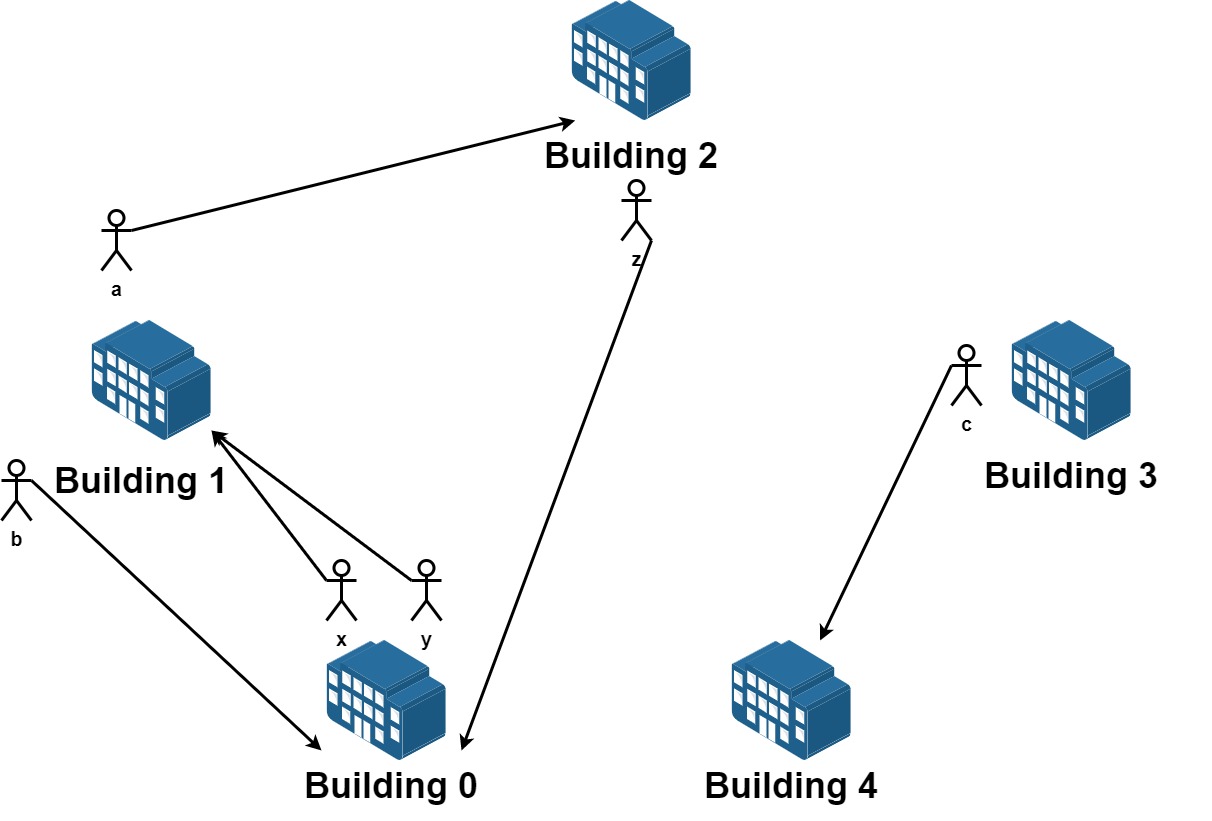
输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出:5
解释:请求列表如下:
从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ,且他想要搬到楼 0 。
从楼 3 离开的员工为 c ,且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼,以满足他们的请求。
我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。
所以最多可以满足 5 个请求。示例 2:
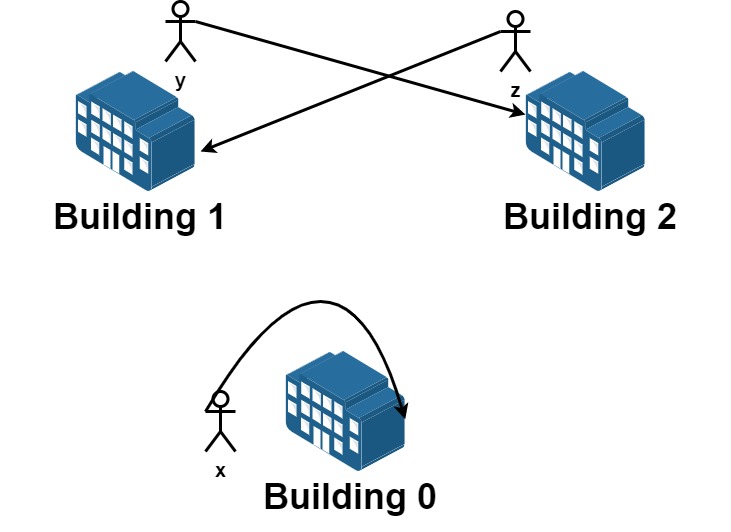
输入:n = 3, requests = [[0,0],[1,2],[2,1]]
输出:3
解释:请求列表如下:
从楼 0 离开的员工为 x ,且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ,且他想要搬到楼 2 。
从楼 2 离开的员工为 z ,且他想要搬到楼 1 。
我们可以满足所有的请求。示例 3:
输入:n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出:4提示:
1 <= n <= 201 <= requests.length <= 16requests[i].length == 20 <= fromi, toi < n
函数签名:
func maximumRequests(n int, requests [][]int) int分析
首先想到,能不能通过统计每栋楼要出去的人out和要进来的人in,最后取每栋楼min(in, out)累加来得到结果?细想不行,会多算。
回溯
数据规模有限,可以用回溯法穷举所有的情况来看结果。对所有 request,穷举每个请求采用和不采用的情况,看看每种情况是不是所有楼进出人数相同。
func maximumRequests(n int, requests [][]int) int {
res := 0
memo := make([]int, n)
var backtrack func(i, used int)
backtrack = func(i, used int) {
if i == len(requests) {
if allZero(memo) && used > res {
res = used
}
return
}
// 不采用 requests[i]
backtrack(i+1, used)
// 采用 requests[i]
v := requests[i]
memo[v[0]]--
memo[v[1]]++
backtrack(i+1, used+1)
memo[v[0]]++
memo[v[1]]--
}
backtrack(0, 0)
return res
}
func allZero(s []int) bool {
for _, v := range s {
if v != 0 {
return false
}
}
return true
}时间复杂度 O(2^m*n),其中 m 为 requests长度,n为楼栋数。穷举所有requests 用弃情况共 2^m,而每种情况为了判定是否满足所有楼进出人数为0,需要遍历 memo。
空间复杂度是 O(n),主要为 memo 数组开辟的空间。
二进制枚举
可以用一个二进制数字来代表采取的请求情况,枚举检查所有情况是否合法(每栋进出人数为0),且统计合法情况下最大的请求数量。
func maximumRequests(n int, requests [][]int) int {
m := len(requests)
res := 0
for mask := 1; mask < 1<<m; mask++ {
cur, ok := check(mask, n, requests)
if ok && cur > res {
res = cur
}
}
return res
}
func check(mask, n int, requests [][]int) (int, bool) {
delta := make([]int, n)
cnt := 0
for i, req := range requests {
if mask&(1<<i) == 0 {
continue
}
cnt++
delta[req[0]]--
delta[req[1]]++
}
for _, v := range delta {
if v != 0 {
return 0, false
}
}
return cnt, true
}时空复杂度同回溯法。