1971. 寻找图中是否存在路径
1971. 寻找图中是否存在路径
| Category | Difficulty | Likes | Dislikes |
|---|---|---|---|
| algorithms | Easy (45.43%) | 69 | - |
有一个具有 n 个顶点的 双向 图,其中每个顶点标记从 0 到 n - 1(包含 0 和 n - 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始,到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false 。
示例 1:
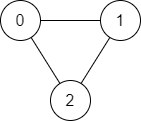
输入:n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出:true
解释:存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2
- 0 → 2示例 2:
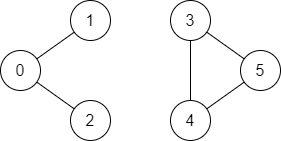
输入:n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出:false
解释:不存在由顶点 0 到顶点 5 的路径.提示:
1 <= n <= 2 * 10^50 <= edges.length <= 2 * 10^5edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1不存在重复边不存在指向顶点自身的边
函数签名:
func validPath(n int, edges [][]int, source int, destination int) bool分析
图论入门问题。可以用 BFS、DFS 或 并查集来解。
BFS 和 DFS 需要先根据 edges 数组构建出图,以快速获取某个节点的邻居节点。
并查集非常巧妙,这里不做过多介绍。
复杂度:
已知节点个数为n,假设边的个数为m,BFS和DFS的时空复杂度都是`O(n+m)`。
并查集的时间复杂度是:`O(n+m*α(m))`,空间复杂度是:`O(m*α(m))`。其中`α(m)`是反阿克曼函数,可以认为是个常数。
实测并查集的复杂度优于BFS或DFS。func validPath(n int, edges [][]int, source int, destination int) bool {
if source == destination {
return true
}
graph := make([][]int, n)
for _, e := range edges {
graph[e[0]] = append(graph[e[0]], e[1])
graph[e[1]] = append(graph[e[1]], e[0])
}
seen := make([]bool, n)
seen[source] = true
q := []int{source}
for len(q) > 0 {
cur := q[0]
q = q[1:]
if cur == destination {
return true
}
for _, v := range graph[cur] {
if seen[v] {
continue
}
seen[v] = true
q = append(q, v)
}
}
return false
}func validPath(n int, edges [][]int, source int, destination int) bool {
if source == destination {
return true
}
graph := make([][]int, n)
for _, e := range edges {
graph[e[0]] = append(graph[e[0]], e[1])
graph[e[1]] = append(graph[e[1]], e[0])
}
seen := make([]bool, n)
var dfs func(int) bool
dfs = func(i int) bool {
if i == destination {
return true
}
seen[i] = true
for _, v := range graph[i] {
if seen[v] {
continue
}
if dfs(v) {
return true
}
}
return false
}
return dfs(source)
}func validPath(n int, edges [][]int, source int, destination int) bool {
if source == destination {
return true
}
uf := make([]int, n)
for i := range uf {
uf[i] = i
}
var find func(int) int
find = func(i int) int {
if uf[i] != i {
uf[i] = find(uf[i])
}
return uf[i]
}
union := func(x, y int) {
x, y = find(x), find(y)
uf[x] = y
}
for _, e := range edges {
union(e[0], e[1])
}
return find(source) == find(destination)
}